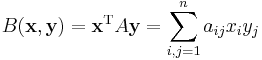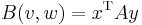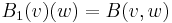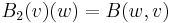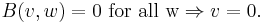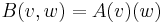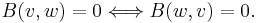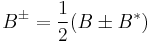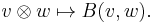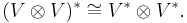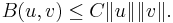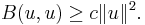Bilinear form
In mathematics, a bilinear form on a vector space V is a bilinear mapping V × V → F, where F is the field of scalars. That is, a bilinear form is a function B: V × V → F which is linear in each argument separately:
Any bilinear form on 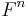 can be expressed as
can be expressed as
where A is an n × n matrix.
The definition of a bilinear form can easily be extended to include modules over a commutative ring, with linear maps replaced by module homomorphisms. When F is the field of complex numbers C, one is often more interested in sesquilinear forms, which are similar to bilinear forms but are conjugate linear in one argument.
Contents |
Coordinate representation
Let 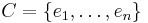 be a basis for a finite-dimensional space V. Define the
be a basis for a finite-dimensional space V. Define the 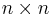 - matrix A by
- matrix A by 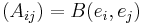 . Then if the
. Then if the 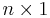 matrix x represents a vector v with respect to this basis, and analogously, y represents w, then:
matrix x represents a vector v with respect to this basis, and analogously, y represents w, then:
Suppose C' is another basis for V, with : 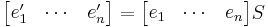 with S an invertible
with S an invertible 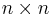 - matrix. Now the new matrix representation for the symmetric bilinear form is given by :
- matrix. Now the new matrix representation for the symmetric bilinear form is given by :
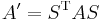
Maps to the dual space
Every bilinear form B on V defines a pair of linear maps from V to its dual space V*. Define 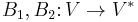 by
by
This is often denoted as
where the ( ) indicates the slot into which the argument for the resulting linear functional is to be placed.
) indicates the slot into which the argument for the resulting linear functional is to be placed.
If either of B1 or B2 is an isomorphism, then both are, and the bilinear form B is said to be nondegenerate. This can only occur if V is finite-dimensional since V* has higher dimension than V otherwise.
If V is finite-dimensional then one can identify V with its double dual V**. One can then show that B2 is the transpose of the linear map B1 (if V is infinite-dimensional then B2 is the transpose of B1 restricted to the image of V in V**). Given B one can define the transpose of B to be the bilinear form given by
If V is finite-dimensional then the rank of B1 is equal to the rank of B2. If this number is equal to the dimension of V then B1 and B2 are linear isomorphisms from V to V*. In this case B is nondegenerate. By the rank-nullity theorem, this is equivalent to the condition that the kernel of B1 be trivial. In fact, for finite dimensional spaces, this is often taken as the definition of nondegeneracy. Thus B is nondegenerate if and only if
Given any linear map A : V → V* one can obtain a bilinear form B on V via
This form will be nondegenerate if and only if A is an isomorphism.
If V is finite-dimensional then, relative to some basis for V, a bilinear form is degenerate if and only if the determinant of the associated matrix is zero. Likewise, a nondegenerate form is one for which the associated matrix is non-singular. These statements are independent of the chosen basis.
Reflexivity and orthogonality
A bilinear form
- B : V × V → F
is reflexive if
Reflexivity allows us to define orthogonality: two vectors v and w are orthogonal with respect to the reflexive bilinear form if and only if :
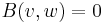 or
or 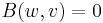
The radical of a bilinear form is the subset of all vectors orthogonal with every other vector. A vector v, with matrix representation x, is in the radical of a bilinear form with matrix representation A, if and only if : 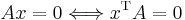 The radical is always a subspace of V. It is trivial if and only if the matrix A is nonsingular, and thus if and only if the bilinear form is nondegenerate.
The radical is always a subspace of V. It is trivial if and only if the matrix A is nonsingular, and thus if and only if the bilinear form is nondegenerate.
Suppose W is a subspace. Define : 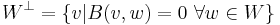
When the bilinear form is nondegenerate, the map 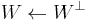 is bijective, and the dimension of
is bijective, and the dimension of 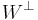 is dim(V)-dim(W).
is dim(V)-dim(W).
One can prove [1] that B is reflexive if and only if it is either:
- symmetric :
 for all
for all 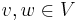 ; or
; or - alternating if
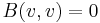 for all
for all 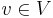
Every alternating form is skew-symmetric (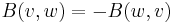 ). This may be seen by expanding B(v+w,v+w).
). This may be seen by expanding B(v+w,v+w).
If the characteristic of F is not 2 then the converse is also true (every skew-symmetric form is alternating). If, however, char(F) = 2 then a skew-symmetric form is the same thing as a symmetric form and not all of these are alternating.
A bilinear form is symmetric (resp. skew-symmetric) if and only if its coordinate matrix (relative to any basis) is symmetric (resp. skew-symmetric). A bilinear form is alternating if and only if its coordinate matrix is skew-symmetric and the diagonal entries are all zero (which follows from skew-symmetry when char(F) ≠ 2).
A bilinear form is symmetric if and only if the maps 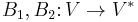 are equal, and skew-symmetric if and only if they are negatives of one another. If char(F) ≠ 2 then one can always decompose a bilinear form into a symmetric and a skew-symmetric part as follows
are equal, and skew-symmetric if and only if they are negatives of one another. If char(F) ≠ 2 then one can always decompose a bilinear form into a symmetric and a skew-symmetric part as follows
where B* is the transpose of B (defined above).
Also if char(F) ≠ 2 then one can define a quadratic form in terms of its associated symmetric form. One can likewise define quadratic forms corresponding to skew-symmetric forms, Hermitian forms, and skew-Hermitian forms; the general concept is ε-quadratic form.
Different spaces
Much of the theory is available for a bilinear mapping
- B: V × W → F.
In this situation we still have linear mappings of V to the dual space of W, and of W to the dual space of V. It may happen that both of those mappings are isomorphisms; assuming finite dimensions, if one is an isomorphism, the other must be. When this occurs, B is said to be a perfect pairing.
In finite dimensions, this is equivalent to the pairing being nondegenerate (the spaces necessarily having the same dimensions). For modules (instead of vector spaces), nondegenerate is a weaker notion: a pairing can be nondegenerate without being a perfect pairing, for instance 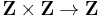 via
via 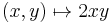 is nondegenerate, but induces multiplication by 2 on the map
is nondegenerate, but induces multiplication by 2 on the map 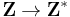
Relation to tensor products
By the universal property of the tensor product, bilinear forms on V are in 1-to-1 correspondence with linear maps V ⊗ V → F. If B is a bilinear form on V the corresponding linear map is given by
The set of all linear maps V ⊗ V → F is the dual space of V ⊗ V, so bilinear forms may be thought of as elements of
Likewise, symmetric bilinear forms may be thought of as elements of S2V* (the second symmetric power of V*), and alternating bilinear forms as elements of Λ2V* (the second exterior power of V*).
On normed vector spaces
A bilinear form on a normed vector space is bounded, if there is a constant  such that for all
such that for all 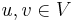
A bilinear form on a normed vector space is elliptic, or coercive, if there is a constant 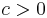 such that for all
such that for all 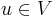
See also
- Bilinear operator
- Multilinear form
- Quadratic form
- Inner product space
- Positive semi definite
- Sesquilinear form
![\begin{array}{l}
\text{1. }B(u %2B u',v) = B(u,v) %2B B(u',v)\text{,} \\[4pt]
\text{2. }B(u,v %2B v') = B(u,v) %2B B(u,v')\text{,} \\[4pt]
\text{3. }B(\lambda u,v) = B(u, \lambda v) = \lambda\,B(u,v)\text{.} \\[4pt]
\end{array}](/2012-wikipedia_en_all_nopic_01_2012/I/81ec79aef39a2b2a3de20e384ddb467d.png)